Apertura

Rosa María Rodríguez Aguilar

José Luis Miguel Castillo González

Alicia Lucrecia Lira Campos

Universidad Autónoma del Estado de México

 

RESUMEN

INTRODUCCIÓN

APRENDIZAJE SIGNIFICATIVO EN LA MATEMÁTICA

LAS TECNOLOGÍAS DE LA INFORMACIÓN Y LA COMUNICACIÓN (TIC) A FAVOR DE UN APRENDIZAJE SIGNIFICATIVO

ANTECEDENTES

Ambientes de aprendizaje

Modalidades del aprendizaje en un ambiente virtual

Software educativo

Clasificación de software educativo (CAI, ICAI, STI)

PROPUESTA DE SOLUCIÓN

Sistemas de enseñanza inteligentes

Metodología para el desarrollo del STI

CONCLUSIONES

Trabajos futuros

Agradecimientos

REFERENCIAS BIBLIOGRÁFICAS

 

RESUMEN

Los problemas de aprendizaje en la matemática a nivel licenciatura se reflejan en el bajo rendimiento escolar o, en el peor de los casos, en el truncamiento de una carrera, por no acreditar asignaturas relacionadas con ésta. Un alto porcentaje de alumnos no cumplen con los requerimientos mínimos en su aprendizaje y, conforme aumentan su complejidad, ocurre su rezago e incremento del índice de reprobación, lo que ocasiona en el alumnado angustia y frustración. La investigación se desarrolla en la Unidad Académica Profesional Nezahualcóyotl (UAP-Nezahualcóyotl) de la Universidad Autónoma del Estado de México (UAEM), con el objetivo de identificar los problemas en el aprendizaje de la matemática en los alumnos de nivel licenciatura y obtener, así, el modelo del sistema tutorial inteligente en matemáticas con la implementación de los diferentes estilos de aprendizaje.

Palabras clave:

Sistema tutor inteligente, tecnologías de la información y la comunicación, aprendizaje significativo en matemática, inteligencias múltiples.

 

INTRODUCCIÓN

Dentro de los objetivos de la educación destaca el preparar al alumno para la vida, enseñarlo a pensar, a que valore la significación del conocimiento y el proceso mismo del aprendizaje, de forma que se estimule cada vez más la independencia, la creatividad y la autorregulación en la obtención de nuevos conocimientos.
El aporte de Ausubel et al. (1987) a la conceptualización del aprendizaje significativo se logra cuando el estudiante puede relacionar los nuevos conocimientos con su experiencia individual (con lo que ya sabe), no de modo arbitrario, sino organizados en estructuras cognitivas.
Teniendo claro que el objetivo final es el descubrimiento del aprendizaje, la única forma es a través de la ejercitación en la solución de tareas contextualizadas, donde más se practica, más se generaliza. La información debe ser organizada en determinados conceptos y categorías para evitar un aprendizaje pasivo y memorístico.

 

APRENDIZAJE SIGNIFICATIVO EN LA MATEMÁTICA

La enseñanza de la matemática juega un papel importante en la formación de individuos que sean capaces de asumir las exigencias científicas y técnicas que demanda el actual desarrollo social.
Son pocas las experiencias referidas en la literatura pedagógica respecto de la utilización del aprendizaje significativo en la enseñanza de la matemática; tampoco abundan en los libros de texto los ejemplos y actividades docentes que muestren cómo trabajar en esa dirección:

....cuando una persona se interesa en aplicar los principios psicológicos para perfeccionar su práctica docente, se encuentra con la carencia de sugerencias concretas para hacerla más efectiva. Lo anterior ocurre porque comúnmente los textos disponibles son muy generales, con amplías revisiones teóricas, pero que extraña vez resaltan las prescripciones teóricas para solucionar los problemas adentro de la clase (Guzmán y Hernández, (Guzmán y Hernández, 1993).

El aprendizaje significativo en la Matemática se presenta a partir de la conexión de sus conocimientos previos relacionados con el contenido matemático a ser procesar, generando la integración de dichos conocimientos, con la nueva información adquirida e incorporación de la metacognición para solucionar la nueva situación presentada. Previamente el estudiante tiene una plena conciencia de los objetivo a alcanzar y conoce las actividades encaminadas a generar la solución del problema presentado, mediante el aprendizaje colaborativo. Entonces se identifican las siguientes ventajas del Aprendizaje Significativo en la enseñanza de la Matemática:

 

• Una mayor motivación por parte de los alumnos en los nuevos conocimientos.
• Aporta al desarrollo de las habilidades, hacia el trabajo individualizado.

 

La edad en la incursión a estos aspectos es básicamente, en la enseñanza básica y en los primeros grados de la enseñanza media.
En suma, para adquirir un aprendizaje significativo es necesario lo siguiente:

 

1. Presentar la conciencia de los conocimientos previos de los alumnos que se encuentran relacionados con los que van a asimilar.
2. Comprobar si los alumnos dominan esos conocimientos, y en el caso que tengan dificultades en los mismos elaborar actividades para su reactivación.
3. Planear actividades diferenciadas orientadas a los alumnos que presentan dificultades.
4. Elaborar una situación de partida, teniendo en cuenta que la misma debe estar vinculada con la práctica, o con otras disciplinas, o con el desarrollo histórico de la propia matemática.
5. Hacer visible la insuficiencia de conocimientos, al no poder resolver la situación presentada con los conocimientos que ellos ya poseen, y a continuación orientarlos para el objetivo.
6. El conocimiento se debe elaborar mediante la articulación del conocimiento anterior con los nuevos conocimientos.
7. Resumir los aspectos más importantes de la clase, así como enfatizar la relación entre el nuevo contenido con los conocimientos previos.

 

LAS TECNOLOGÍAS DE LA INFORMACIÓN Y LA COMUNICACIÓN (TIC) A FAVOR DE UN APRENDIZAJE SIGNIFICATIVO

En este nuevo siglo, resulta de particular trascendencia que se analicen las múltiples facetas de la combinación estudiante-profesor-TIC en el proceso de enseñanza-aprendizaje, y los cambios que esta incursión traerá consigo. La vinculación entre la educación y las TIC constituye hoy una práctica de formación integral del estudiante mediante una educación que sea reflexiva y enriquecedora.

Es conveniente promover y difundir en los diferentes niveles del sistema educativo la inserción de las TIC en la educación para el logro de aprendizajes significativos; fomentar la necesidad de un cambio en las metodologías tradicionales que permita divulgar la enseñanza personalizada en el proceso de aprendizaje; e impulsar la creación de programas que faciliten la presentación del contenido de las más diversa formas.

Algunos de los elementos que garantizan el éxito de un aprendizaje significativo con el uso de las TIC, y de la computadora en particular, en el proceso de enseñanza-aprendizaje de la matemática son los siguientes:

 

• Actúa como elemento motivacional. El estudiante se siente atraído por la computadora.
• Hace que gane confianza como ser intelectual y aprecie su actividad como algo importante y no como el cumplimiento de un deber.

• Propicia el desarrollo de un aprendizaje personalizado, al posibilitar al estudiante avanzar según su propio ritmo de aprendizaje.
• Facilita la interacción hombre-máquina, al presentar de manera visual la interfaz de la computadora por medio de gráfica de figuras, imágenes, animaciones, simulaciones que proporcionan cierto grado de realidad psicológica y ayudan a que la mente alcance los objetivos de una forma más adecuada, amena y atractiva.
• Permite al estudiante aprender de sus errores y minimiza la sensación de fracaso que siente al no lograr el éxito esperado.

•  Hace posible que el estudiante aprenda descubriendo, al estimular la independencia y el autoaprendizaje.
• Estimula el trabajo en equipo.

 

Para el logro de lo anterior, el educador en matemática en nuestros tiempos debe poseer conocimientos sólidos en las siguientes áreas:

 

• En la propia matemática.
• En la didáctica de la matemática.
• En las TIC.
• En las didácticas específicas para el uso efectivo de las TIC.
• En una cultura integradora de estas nuevas herramientas.

 

Por ello, la propuesta es un instrumento computacional con referente pedagógico capaz de servir como herramienta en el proceso de enseñanza-aprendizaje (Cuevas, 2003). Este trabajo se divide en los siguientes apartados: revisión de antecedentes para contextualizar la aplicación de las TIC en la implementación de un sistema capaz de ayudar en la adquisición de un conocimiento significativo en el estudio de las matemáticas; análisis del instrumento de evaluación realizado a los alumnos de las diferentes licenciaturas que ofrece la UAP-Nezahualcóyotl para identificar sus carencias en la resolución; y a partir de ello, implementar en el sistema tutor inteligente las dificultades surgidas integrando en su diseño los distintos estilos de aprendizaje por medio de las inteligencias múltiples de Gardner.

 

ANTECEDENTES

Proceso de enseñanza-aprendizaje
Los factores que inciden en el aprendizaje son: actitudes, aptitudes y contenidos (ver figura 1). Por lo anterior, se pensó que si una persona tenía los métodos y contenidos y quería saber, podía aprender; sin embargo, en 1952 Piaget empezó a hablar del desarrollo de los procesos de pensamiento; de allí surgió la idea de que la capacidad intelectiva influye en el aprendizaje, además de los factores anteriores y del contexto. Todo lo que el estudiante oye, se olvida, lo que ve, se recuerda y lo que hace, se aprende (Riquelme, 2008).

 

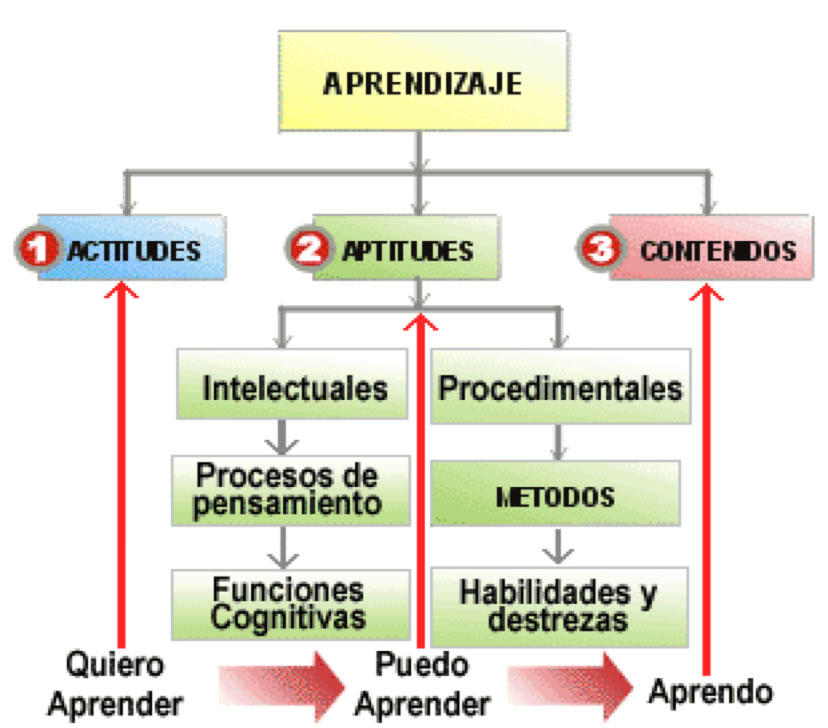Figura 1. Factores en el aprendizaje.

 

La incorporación de nuevas políticas de enseñanza requiere adecuar planes de estudio, temarios y métodos. El alumno debe convertirse en parte activa y representar el centro del proceso de aprendizaje; esto implica un cambio en la concepción de un modelo educativo (Mateo et al., 2007).

 

Ambientes de aprendizaje

La enseñanza se encuentra matizada por el uso de las TIC, entre ellas la computadora ha desempeñado una función preponderante por sus ventajas, tanto para la explicación de conceptos como para su apropiación. En la medida en que avanza la tecnología, se buscan métodos más efectivos para el proceso educativo. Se infiere que para cada cambio de la informática se asocia una didáctica que apoya la práctica docente (Moreno, 2004).

 

Modalidades del aprendizaje en un ambiente virtual

Es importante destacar que las modalidades del aprendizaje sirven para dar una idea de los componentes necesarios y útiles para diseñar un ambiente de aprendizaje. Rivera (1989) las categoriza como se muestra en la tabla 1.

 

Tabla 1. Modalidades de aprendizaje.

 

Hay muchos tipos de materiales educativos computarizados, cada uno de ellos pensado para desempeñar funciones específicas; es posible saber si cumplen con los requerimientos propios del tipo al que pertenecen y si cada método utilizado tiene un papel diferente.

 

Software educativo

El software educativo aparece con la difusión de las computadoras en la enseñanza de acuerdo con tres esquemas de trabajo: computadoras utilizadas como tutores (enseñanza asistida por computadoras (CAI), integrando la inteligencia artificial (ICAI) y como herramienta, con el surgimiento de los sistemas tutoriales inteligentes (STI) (Self, 1999).

 

Clasificación de software educativo (CAI, ICAI, STI)

En esta categoría entran programas de instrucción asistida por computadora (CAI), aprendizaje apoyado en la computadora (CAL y CALM), los sistemas tutoriales inteligentes (STI) y aprendizaje colaborativo soportado por computadora (CSCL). Cada una de estas modalidades centra su atención en los procesos en los que el estudiante desarrolla problemas y ejercicios para adquirir una mejor comprensión de conceptos matemáticos; así, el modelo es lo que cambia para cada tipo de sistema. Destacan, además, los STI que implementan un modelo de enseñanza a través de un mecanismo de evaluación de respuestas del estudiante a preguntas propuestas por el sistema (Cuevas, 1999; Burns & Capps, 1988).

 

PROPUESTA DE SOLUCIÓN

Sistemas de enseñanza inteligentes

Con el fin de integrar las nuevas tecnologías y producir una herramienta que permita una adaptación a un entorno dinámico, siendo este último el estado cognitivo del estudiante, se propone desarrollar un STI con características reactivas (Laureano & De Arriaga, 2000; Laureano,Terán-Gilmore & Rodríguez, 2005) y que incluye el componente interactivo de comunicación integradora asociada a las nuevas tecnologías dentro de su interfaz (Laureanoet al., 2010). A continuación, se detalla cada uno de los componentes.

• Modelo del estudiante: está constituido por la base de datos que representa el estado cognitivo del estudiante y el entorno que se pretende cambiar.
• Modulo experto: es el lugar donde se acumula el conocimiento del experto.
• Modulo tutorial: determina las estrategias pedagógicas e instruccionales del sistema.
• La interfaz: puede ser considerada como un entorno de simulación en el sentido de que es el lugar donde tienen representación las salidas y entradas del sistema. Su compromiso básico es la comunicación entre el sistema y el estudiante, aunque al ser el medio de salida de las acciones del STI, también tiene una responsabilidad didáctica (Laureano, Terán-Gilmore & Rodríguez, 2005; Laureanoet al., 2009).

 

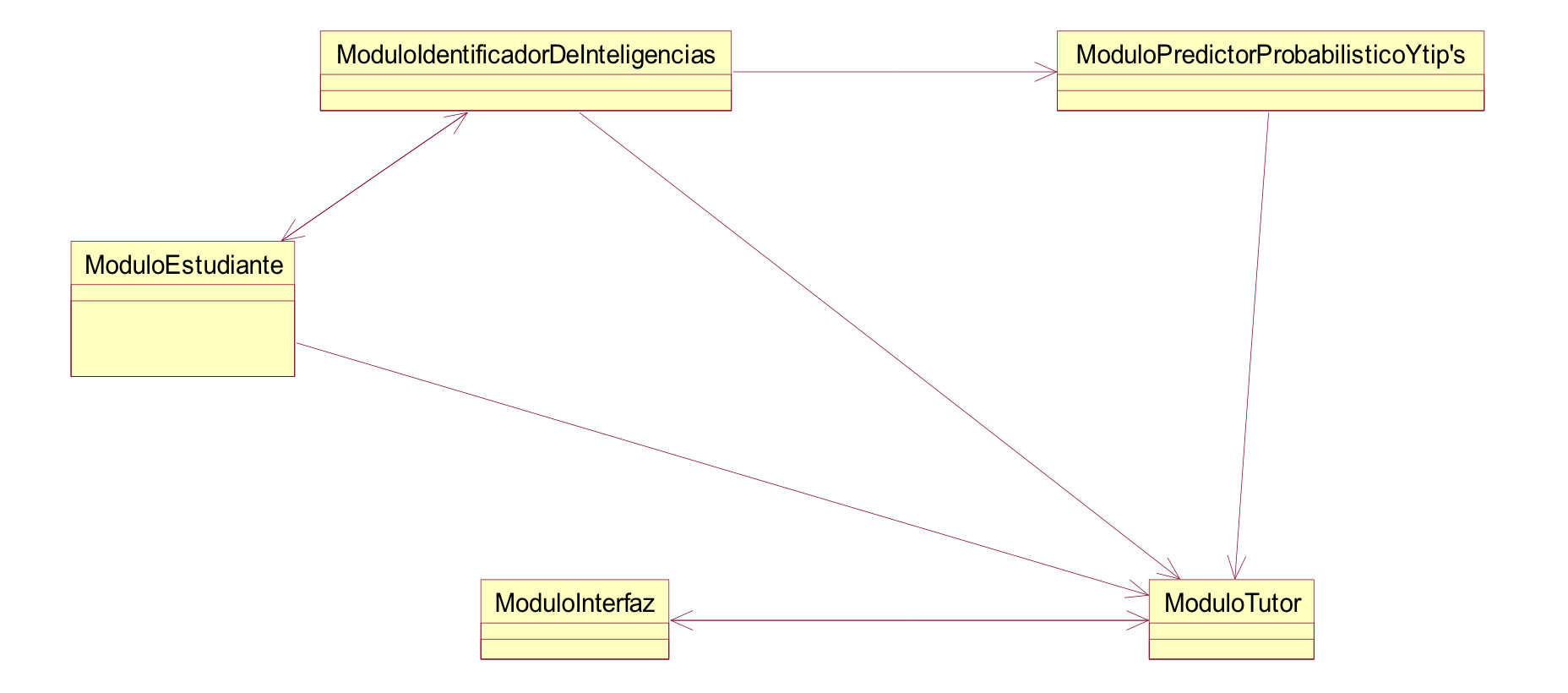Figura 2. Arquitectura de sistema tutorial inteligente.

 

Uno de los objetivos de la inteligencia artificial es simular la manera en que piensan y actúan los seres vivos, principalmente el hombre, es decir, se busca el confort del ser humano. En ese sentido, los STI buscan un proceso de enseñanza-aprendizaje uno a uno, en que los dos agentes sistema-usuario se transforman y adaptan (Laureano & De Arriaga, 2000; Laureanoet al., 2010). Así, la inteligencia artificial cobra una nueva importancia al ser parte de la tecnología que permite, a través del uso de estas herramientas, la adaptación de los distintos sistemas al ser humano.

En el caso de los recursos educacionales, la contribución a los STI se refiere a las técnicas de aprendizaje que soportan el proceso de resolución de problemas y diagnosticar los errores del estudiante, en el caso específico del álgebra elemental. Este dominio se determinó con base en el análisis del examen diagnóstico aplicado en la UAP-Nezahualcóyotl, donde se identificaron las áreas iniciales de conflicto de los examinados; se considera que el alumno debe apropiarse de su conocimiento de manera gradual, y empezar precisamente en el área que le crea conflicto y de este modo incrementar el grado de complejidad con base en su madurez cognoscitiva.

 

Metodología para el desarrollo del  STI

El enfoque metodológico del presente trabajo inició con una primera fase de estudio cualitativo y cuantitativo, derivado de un examen diagnóstico de matemáticas aplicado a los alumnos de las licenciaturas en Comercio Internacional, Educación para la Salud e Ingeniería en Sistemas Inteligentes; en total fueron 600 alumnos de primer semestre, tercero y quinto de la UAP-Nezahualcóyotl de la UAEM. El contenido incluyó temas de aritmética, geometría y trigonometría de nivel medio superior. La evaluación de este dominio reconoció una serie de deficiencias, las cuales son por una falta de madurez cognitiva en los conocimientos de álgebra básica. Para la implementación del STI, se utilizará como propuesta de desarrollo de sistemas de calidad la metodología de la ingeniería del software, que especifica los siguientes pasos en forma muy general: análisis, diseño, implementación y pruebas del sistema.

En la etapa deanálisis se tiene el objetivo de identificar con precisión las necesidades de información de una organización y establecer la alternativa de solución más conveniente para satisfacerla: resolver la problemática de aprendizaje en el área de matemáticas de la UAP-Nezahualcóyotl. Este análisis se basa en la información recopilada, como la aplicación del examen diagnóstico, el análisis de los resultados y, derivado de lo anterior, la descripción de las características que debe contener el sistema, tanto de software como de hardware.

La etapa de diseño establece los aspectos lógicos y físicos de las salidas, modelos de organización y representación de datos, entradas y procesos del sistema, considerando las bondades y limitaciones de los recursos disponibles en satisfacer los requerimientos del análisis.
La etapa de implementación tiene el propósito de programar el sistema con base en el lenguaje de computación más adecuado, así como los procedimientos que tendrá que realizar la computadora durante la manipulación de los datos para obtener los resultados deseados.

Con pruebas exhaustivas del sistema se garantiza su funcionamiento apropiado. Se crea una muestra de datos que reúnan las diversas variedades de casos posibles durante la operación y se diseñan datos erróneos para verificar que los detecte el sistema. Las siguientes fases en el desarrollo del STI están basadas en la propuesta de Laureano & De Arriaga (2000):

 

• Diseño del gráfico de conocimiento utilizando como metas (representaciones de los nodos) los objetivos instruccionales.
• Diseño del modelo cognitivo que permita citar las características del usuario, a fin de detectar el tipo de inteligencia que permita adaptar el material didáctico.
• Diseño de distintos escenarios que son parte de la interfaz que faciliten una detección de las distintas inteligencias.
• Dentro de estos escenarios se hizo un análisis previo de cada reactivo, y se ponderó por medio de pesos qué tipo de inteligencia corresponde a cada uno. Se tomaron como variables cuantificables las distintas partes que tuvieran una relevancia en cada uno de los reactivos, como lógica-matemática, auditivo o musical verbal o lingüista y visual; de hoy en adelante se denotará con las siglas MALVI. Posteriormente, se aplicará la teoría de inferencias bayesiana de acuerdo con el teorema de Bayes, cuya aplicación permite determinar el algoritmo necesario para el análisis de cada reactivo y el diseño de escenarios más adecuado, dependiendo del tipo de usuario.
• Diseño del proceso de enseñanza-aprendizaje desde dos perspectivas: la inteligencia relacionada con el tipo de conocimiento y la inteligencia identificada en el usuario.
• Adaptación del motor de inferencia reactivo que se integrará al proceso de enseñanza-aprendizaje a través de los escenarios.

 

Diseño de la interfaz que constituirá las técnicas de diagnóstico, y estrategias de tácticas y técnicas instruccionales (ver figura 3).

 

Figura 3. Arquitectura general del sistema.

 

El módulo del estudiante está constituido por la base de datos que representa el estado cognitivo del estudiante, determinado por el módulo identificador de inteligencias que permite definir el perfil del estudiante de acuerdo con las inteligencias a tratar en el sistema MALVI. Esto se podrá establecer por medio de un cuestionario, junto con el módulo predictor probabilístico y Tips, los cuales formarán el módulo experto, en el que se encuentra acumulado el conocimiento del experto; el módulo tutor, que fija las estrategias pedagógicas e instruccionales del sistema; y el módulo interfaz, encargado de simular las entradas y salidas.
Estos dos submódulos se muestran gráficamente en la figura 4, los cuales constituyen el módulo predictor probabilístico y Tips, en el cual el submódulo probabilísticos de reactivos contendrá el conjunto de reactivos ya diferenciados por cada una de las inteligencias a tratar en el presente trabajo; el submódulo Tips incluirá las diferentes sugerencias según las estrategias pedagógicas más adecuadas diferenciadas por el perfil del usuario (Rodríguezet al., 2010).

 

Figura 4. Módulo predictor probabilístico y Tips.

 

CONCLUSIONES

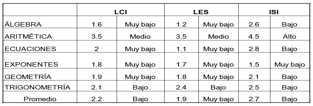
A partir del estudio cualitativo se tienen los siguientes resultados del análisis del examen diagnóstico aplicado a las dos licenciaturas y la ingeniería (ver tabla 2):

• Los alumnos de la licenciatura en Educación para la Salud y la licenciatura en Comercio Internacional muestran una tendencia de media a muy baja en el conocimiento general de las matemáticas básicas y son superados por los de Ingeniería en Sistemas Inteligentes, con 13% de su desempeño.
• Para las tres licenciaturas el conocimiento alto, que corresponde a la mayor calificación, fue adquirido por los alumnos de Ingeniería en Sistemas Inteligentes en el rubro de aritmética, seguido del conocimiento en trigonometría (bajo), también por alumnos de esta carrera.
• El conocimiento de álgebra obtuvo cuatro ponderaciones de nulo conocimiento para la licenciatura en Educación para la Salud y una ocasión para Comercio Internacional, que resultó ser el área de menor conocimiento matemático.
• El conocimiento alto, que corresponde a la calificación más alta, se presenta en el rubro de la aritmética, en el que destacan los alumnos de ingeniería, similar a los alumnos de Comercio Internacional y Educación para la Salud. El conocimiento matemático de álgebra oscila en los niveles de muy bajo a bajo.
• A pesar de que el valor promedio es superior en ingeniería, no existen diferencias significativas entre los alumnos de las licenciaturas analizadas, aunque su posición se encuentra dentro de la misma categoría de bajo conocimiento, pero ubicado en el límite superior de dicho intervalo.

 

Tabla 1. Modalidades de aprendizaje.

 

Trabajos futuros

Derivado del análisis anterior y con base en la propuesta mostrada, nos encontramos en la etapa final de la programación del sistema tutorial, con el cual se pretende probar que, efectivamente, el uso de las TIC en la implementación de los sistemas tutores inteligentes son una herramienta de apoyo en los procesos de aprendizaje, tomando como referencia en este caso las inteligencias múltiples de Gardner. Hay que tener en cuenta que el objetivo principal es reducir el problema del aprendizaje poco significativo de la matemática en la UAP- Nezahualcóyotl, UAEM, que arrastran los alumnos por la deficiente educación previa, que repercute de manera directa en su educación universitaria.

 

Agradecimientos

Este trabajo fue realizado gracias al apoyo recibido de la Secretaría de Investigación y Estudios Avanzados de la UAEM, como parte del proyecto de investigación “Modelo de un tutor inteligente aplicado al área de las matemáticas”, con clave 2657/2008.

 

REFERENCIAS BIBLIOGRÁFICAS

Ausubel, D. et al. (1987). Psicología. Un punto de vista cognoscitivo, 2ª. ed. México: Trillas.

Burns, H. & Capps, Ch. (1988). Foundations of Intelligent Tutoring Systems (M. Polson & J.

Richardson [eds.]). EUA: Lawrence Erlbaum Assosiates Publishers.

Cuevas, A. (1999). Una propuesta didáctica para la enseñanza de las matemáticas, basada en la psicología de Jean Piaget. México: Departamento de Matemática Educativa, Cinvestav- IPN.

_____(2003). Una propuesta didáctica para la enseñanza de las matemáticas (manuscrito). México: Departamento de Matemática Educativa, CINVESTAV-IPN.

Guzmán, J. y Hernández, G. (1993). Implicaciones educativas de seis teorías psicológicas. La Habana: UNAM.

Laureano, A. & de Arriaga, F. (2000). Reactive Agent Design for Intelligent Tutoring Systems. Cybernetics and Systems, an International Journal, vol. 31, núm. 1, pp. 1-47.

Laureano, A., Terán-Gilmore, A. & Rodríguez, R. (2005). Cognitive and Affective Interaction in a Pedagogical Agent. Memorias del XVIII Congreso Nacional y IV Congreso Internacional de Informática y Computación de la ANIEI, 26-28 de octubre, Torreón, Coahuila. Recuperado de http://delfosis.uam.mx/~ana/

Laureano, A. et al. (2009). Hacia interfaces inteligentes. En Avances de las mujeres en las ciencias, las humanidades y todas las disciplinas. Sustentabilidad, aire, agua, fuego y tierra (pp. 237-246). CYAD/UAM-A.

Laureano, A. et al. (2010). Cognitive-Operative Model of Intelligent Learning Systems Behavior. Interactive Learning Environments, vol. 18, núm.1, pp. 11-38.

Mateo, M. et al. (2007). Una nueva metodología docente para un autoaprendizaje bajo entornos virtuales. Universitat Rovira i Virgili.

Moreno, M. (2004). Historias de innovación educativa. "Un documento conmemorativo".  México: INNOVA.

Riquelme, M. (2008). Lineamientos para la propuesta de un modelo pedagógico desde la perspectiva del aprendizaje significativo. Recuperado el 12 de junio de 2009 de http://www.vulcano.lasalle.edu.co/~docencia/Aprendizaje_Sig_general.htm

Rivera, E. (1989). Aprendizaje asistido por computadora. San Juan, Puerto Rico: Librotex.

Rodríguez, R. et al. (2010). Diseño de un ambiente virtual de aprendizaje: un enfoque reactivo a las distintas inteligencias. En XXIII Congreso Nacional y IX Congreso Internacional de Informática y Computación ANIEI 2010 (pp. 494-505), 13 al 15 de octubre, Puerto Vallarta, Jalisco, México.

Self, J. (1999). The defining characteristics of intelligent tutoring systems research: ITS care, precisely. Journal of Artificial Intelligence in Education, vol. 10, núm. 3-4, pp. 350-364.